To use WC-LR-Cournot, you will have to install NetLogo 5.3.1 (free and open source) and download the model itself. Unzip the downloaded file and click on wc-lr-cournot.nlogo
WC-LR-Cournot is a model designed to analyse the Win-Continue, Lose-Reverse rule in Cournot oligopolies. This section gives an informal and brief overview of WC-LR-Cournot. We use bold red italicised arial font to denote parameters (i.e. variables that can be set by the user). Any parameter value can be changed at runtime, with immediate effect on the dynamics of the model.
In WC-LR-Cournot, there are num-firms firms which provide a homogeneous good or service and have to choose their production level qi. The market price p depends on the total amount SUMi(qi) produced by the firms, and -in principle- it is the same for all firms. (The model can be parameterised so there can be small differences among the prices that each company receives for its products.) The process advances in discrete time steps and at every time step the companies have to simultaneously choose whether to increase or decrease their production level qi. The decision rule considered here can be simply stated as: repeat your last action (i.e. an increase or a decrease in production) if your profits have grown; otherwise, choose the opposite action. This simple rule has been named "Win-Continue, Lose-Reverse" (WCLR) by Huck et al. (2003), who conducted a thorough study of its convergence properties in symmetric Cournot oligopolies.
This section explains the formal model that WC-LR-Cournot implements. The information provided here should suffice to re-implement the same formal model in any sophisticated enough modelling platform.
The considered model is a Cournot duopoly in which at every time step t (t = 0, 1, ...) each company i (i = 1, 2, ... ,num-firms) chooses a production level or quantity [qi]t. In principle, the market price [p]t is the same for all companies and it depends on the total quantity produced by all firms, according to the following formula:
[p]t = p0 - a·SUMi([qi]t).
The amount [qi]t is produced on period t with the cost function C(q):
C(q) = c0 + c1·q + c2·q2.
The profit for each company on period t is
[πi]t = [pi]t·[qi]t - C([qi]t).
Incremental values are naturally defined as [Δπi]t := [πi]t - [πi]t-1, and initial values at time step 0 are [Δπi]0 = 0, and [Δqi]0 = 0.
Let us also define [si]t := SIGN([Δqi]t·[Δπi]t). Note that [si]t is equal to +1 if the last changes in [qi]t and [πi]t took place in the same direction, and [si]t is equal to -1 if such changes went in opposite directions.
For each company i, the production levels are calculated as [qi]t+1 = MAX([qi]t + [Δqi]t+1, 0), starting with a random initial positive production level [qi]0 at time step 0. (To be precise, [qi]0 is a random multiple of step in the range [0, (p0 / (a * num-firms)].) The decision rule WCLR used to calculate the production increments [Δqi]t+1 is implemented as follows:
WCLR Rule:
It is also assumed that the process includes three types of "noise":
[ci]t = C([qi]t)·(1 + cost-variability·random-distribution)
where random-distribution is a continuous uniform random variable with range [-1 , 1] if random-distribution = Uniform [-1, 1], or a normal distribution N[0, 1/3] with mean 0 and variance 1/3 if random-distribution = Normal [0, 1/3].
[pi]t = [p]t·{1 + price-variability·(alpha·COMMON + (1 - alpha)·INDIVIDUAL)}
where [p]t is the price that corresponds to the total level of output using the inverse demand function described above, COMMON is a random sample from the distribution dictated by random-distribution which is shared by all firms in the market in each time-step, and INDIVIDUAL is a random sample from the distribution dictated by random-distribution which is specific to each firm in the market in each time-step.
This modified model represents small differences in the price that each company gets for its products, which can be due to a number of different reasons, such as random deviations in the quality of the products of a company with respect to the average quality, different times of arrival at the market (which would allow for some variability in demand), different intermediaries with variable commissions, existence of local markets (which would allow for some variability in price), etc.
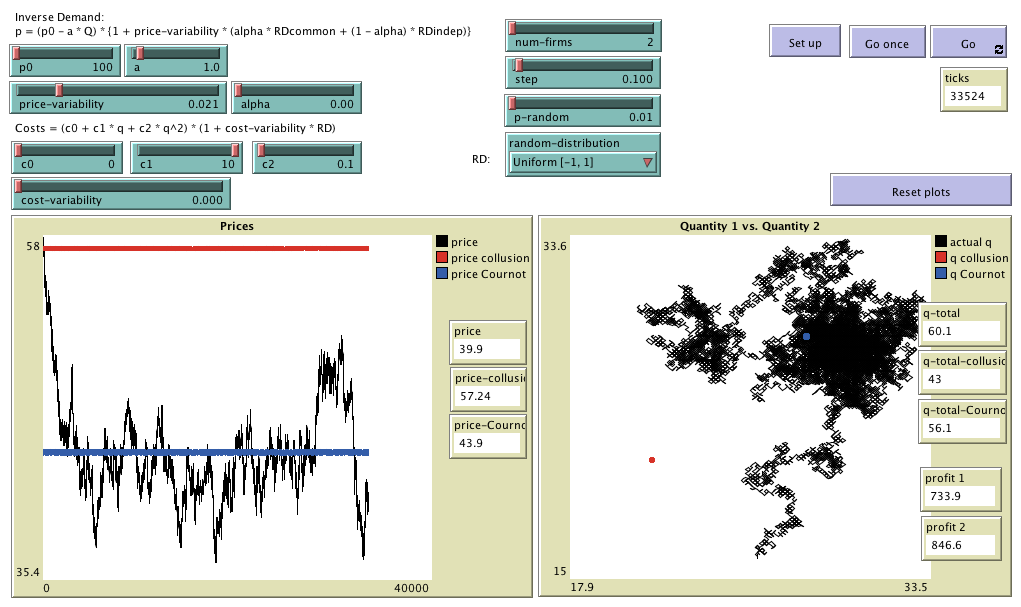
wc-lr-cournot is a model designed to analyse the "Win-Continue, Lose-Reverse" rule in Cournot oligopolies.
Copyright (C) 2014 Segismundo S. Izquierdo & Luis R. Izquierdo
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.
Contact information:
Segismundo S. Izquierdo
University of Valladolid, Spain.
e-mail: segis@eii.uva.es
This program has been designed and implemented by Segismundo S. Izquierdo & Luis R. Izquierdo.