The "Win-Continue, Lose-Reverse" rule in a Bertrand-like duopoly

Segismundo S. Izquierdo & Luis R. Izquierdo

HOW TO INSTALL THE MODEL

To use WC-LR-Bertrand, you will have to install NetLogo 5.3.1 (free and open source) and download the model itself. Unzip the downloaded file and click on wc-lr-bertrand.nlogo

DESCRIPTION OF THE MODEL

WC-LR-Bertrand is a model designed to analyse the Win-Continue, Lose-Reverse rule in duopolies with differentiated products where firms compete in prices. This section explains the formal model that WC-LR-Bertrand implements. The information provided here should suffice to re-implement the same formal model in any sophisticated enough modelling platform. We use bold red italicised arial font to denote parameters (i.e. variables that can be set by the user). Any parameter value can be changed at runtime, with immediate effect on the dynamics of the model.

The considered model is a (Bertrand-like) duopoly with differentiated products in which the decision variable is the price level. The process advances in discrete time steps and at every time step t (t = 0, 1, ...) the two companies have to simultaneously choose whether to increase or decrease their price level [p_i]_t. The decision rule considered here can be simply stated as: repeat your last action (i.e. an increase or a decrease in price) if your profits have grown; otherwise, choose the opposite action. This simple rule has been named "Win-Continue, Lose-Reverse" (WCLR) by Huck et al. (2003), who conducted a thorough study of its convergence properties in symmetric Cournot oligopolies.

In WC-LR-Bertrand, each company i (i = 1, 2) faces a market demand [q_i]_t which depends on the prices chosen by both companies, according to the following formula:

[q_i]_t = MAX(q0 - ai·[p_i]_t + aj·[p_j]_t, 0)

where i ≠ j.

The amount [q_i]_t is produced on period t with the cost function C(q):

C(q) = c0 + c1·q + c2·q².

The profit for each company on period t is

[π_i]_t = [p_i]_t·[q_i]_t - C([q_i]_t).

Incremental values are naturally defined as [Δπ_i]_t := [π_i]_t - [π_i]_t-1, and initial values at time step 0 are [Δπ_i]₀ = 0, and [Δp_i]₀ = 0.

Let us also define [s_i]_t := SIGN([Δp_i]_t·[Δπ_i]_t). Note that [s_i]_t is equal to +1 if the last changes in [p_i]_t and [π_i]_t took place in the same direction, and [s_i]_t is equal to -1 if such changes went in opposite directions.

For each company i, the price levels are calculated as:

[p_i]_t+1 = MAX([p_i]_t + [Δp_i]_t+1, c1).

Note that we impose that the price should be no less than the minimum marginal cost of the firms, c1. Initial value [p_i]₀ at time step 0 is a random multiple of step in the range [0, (q0 / ai].) The decision rule WCLR used to calculate the price increments [Δp_i]_t+1 is implemented as follows:

WCLR Rule:

• If t = 0 or [s_i]_t = 0, then [Δp_i]_t+1 takes one random value out of the set {-step, 0, step}, where step is the step size.
• Otherwise, [Δp_i]_t+1 = step·[s_i]_t.

Noise

It is also assumed that the process includes three types of "noise":

• Decision noise: With a small probability p-random for each company in every period, the company will deviate from the value prescribed above for [Δp_i]_t+1 and will take a random choice among {-step, 0, step}. This "decision noise" can represent occasional mistakes or experimentation.
• Cost noise, characterised by the parameter cost-variability, and implemented by altering each firm's base cost according to the following formula:

  [c_i]_t = C([q_i]_t)·(1 + cost-variability·U[-1,1])

  where U[-1,1] is a continuous uniform random variable with range [-1 , 1].

• Demand noise, characterised by the parameter demand-variability, and implemented by altering the demand of each firm [q_i]_t according to the following formula:

  [q_i]_t = MAX((q0 - ai·[p_i]_t + aj·[p_j]_t)·{1 + demand-variability·(alpha·U[-1,1]_COMMON + (1 - alpha)·U[-1,1]_INDIVIDUAL)}, 0)

  where U[-1,1]_COMMON is a continuous uniform random variable with range [-1 , 1] which is shared by the two firms in the market in each time-step, and U[-1,1]_INDIVIDUAL is a continuous uniform random variable with range [-1 , 1] which is specific to each firm in the market in each time-step. Extreme value alpha = 0 represents completely uncorrelated perturbations, whilst extreme value alpha = 1 represents full correlation between the demand perturbations received by each firm (potentially due, for instance, to seasonal demand variability in both products, or global factors affecting the demand of both products in the same way).

HOW TO USE IT

Buttons

• Set up: Initializes the model.
• Go once: Pressing this button will run the model one time-step only.
• Go: Pressing this button will run the model until this same button is pressed again.
• Reset plots: Pressing this button will reset the two plots with an adequate scale. Useful when some parameters have been changed at runtime

PLOTS AND MONITORS

Plots

• Prices: Time series of the prices in the market, of the collusion price and of the Nash price.
• Price 1 vs. Price 2: Time series of the prices set by the two firms in the market, of the prices corresponding to the collusion equilibrium, and of the prices corresponding to the Nash equilibrium.

Monitors

• ticks: Number of time-steps that have gone by.

• price-collusion: Price corresponding to the collusion equilibrium with the current values for the parameters.
• price 1: Price set by firm 1 in the current time-step.
• price 2: Price set by firm 2 in the current time-step.
• price-Nash: Price corresponding to the Nash equilibrium with the current values for the parameters.

• q 1: Quantity sold by firm 1 in the current time-step.
• q 2: Quantity sold by firm 2 in the current time-step.
• profit 1: Profit of firm 1 in the current time-step.
• profit 2: Profit of firm 2 in the current time-step.

LICENCE

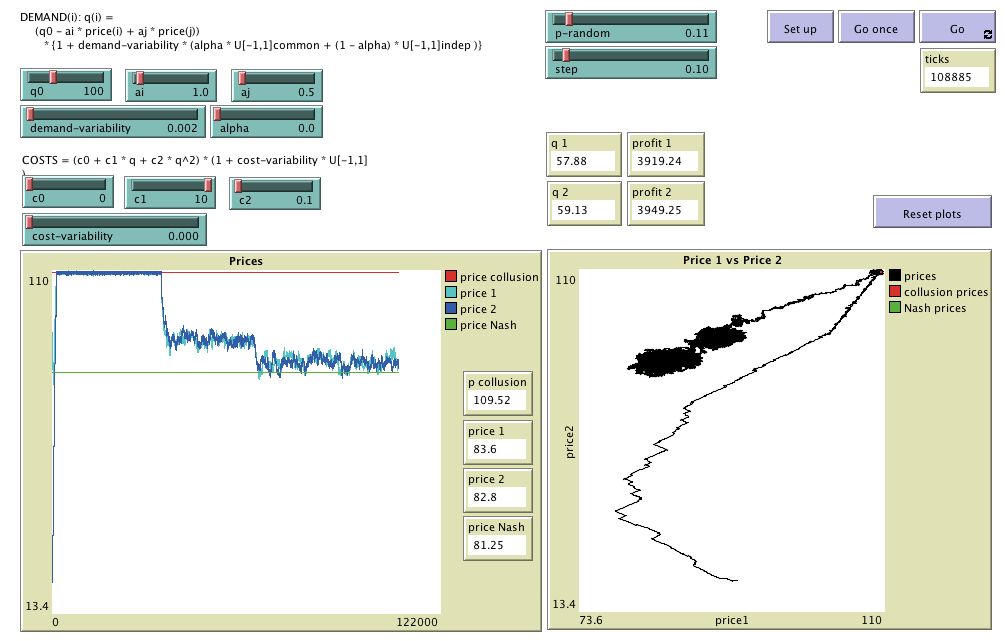
wc-lr-bertrand is a model designed to analyse the Win-Continue, Lose-Reverse rule in a Bertrand-like duopoly.
Copyright (C) 2014 Segismundo S. Izquierdo & Luis R. Izquierdo

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.

Contact information:
Segismundo S. Izquierdo
University of Valladolid, Spain.
e-mail: segis@eii.uva.es

MODELLERS

This program has been designed and implemented by Segismundo S. Izquierdo & Luis R. Izquierdo.

REFERENCES

• Huck S, Normann HT, Oechssler J (2003) Zero-knowledge cooperation in dilemma games. J. Theor. Biol. 220(1): 47-54