To use StandingOvation, you will have to install NetLogo 5.3.1 (free and open source) and download the model itself. Unzip the downloaded file and click on StandingOvation.nlogo
The Standing Ovation model proposed by Miller and Page (2004) illustrates a familiar decision-making problem: at the end of a performance the audience begins to applaud. The applause builds and a few members of the audience decide to stand up in enthusiastic recognition. In this situation every other member of the audience must decide whether to join the standing individuals in their ovation, or else remain seated. It is not a trivial decision; imagine, for example, that you initially decide to stay down quietly but then find yourself surrounded by people standing and clapping vigorously. It seems plausible that you may feel awkward, change your mind and end up standing up, saving yourself a significant dose of potential embarrassment. Analogously, you probably wouldn't enjoy being the only person standing and clapping alone in the middle of a crowded auditorium of seated people.
Miller and Page (2004) explore this problem using a computational model to show the advantages of agent-based modelling. They correctly point out that the model differs from the real world in that people in the real world eventually leave the auditorium. This model is also discussed by de Marchi (2005, pp. 6-10) and by Miller and Page (2007, pp. 10-14)
Here we analyse the computational model described by Miller and Page (2004) in section 6 of their paper. In this model there is a square auditorium L×L crowded with agents. At the conclusion of the performance, each agent evaluates the performance's quality. Agent i's perception of the quality of the show is a random floating-point number in the interval [0, 1] and is denoted qi. If this value qi is greater than a certain threshold (with default value equal to 0.5) the agent decides to stand up. Once every agent has assessed the quality of the show and has acted accordingly, every agent reviews her current decision by observing the behaviour of her neighbours and following a majority rule: if the majority of her neighbours are showing a different behaviour, she changes her mind and follows the prevalent behaviour in her neighbourhood –standing or seating– [1]. This reviewing process repeats indefinitely.
Miller and Page (2004) consider two types of neighbourhoods: "five neighbours" and "conical neighbourhood". In the first one, each agent looks at the two agents on either side and the three agents on the row ahead. In the "conical neighbourhood", each agent looks at the two agents on either side, the three agents on the first row ahead, the five agents on the second row ahead and so on.
Another important aspect of this model is the scheduling of events within each time-step (i.e. the temporal order in which agents make their decisions). Miller and Page (2004) propose three timing alternatives, but here we only consider two of them in detail:
StandingOvation.nlogo is a NetLogo (Wilensky 1999) implementation of Miller and Page's (2004) model.
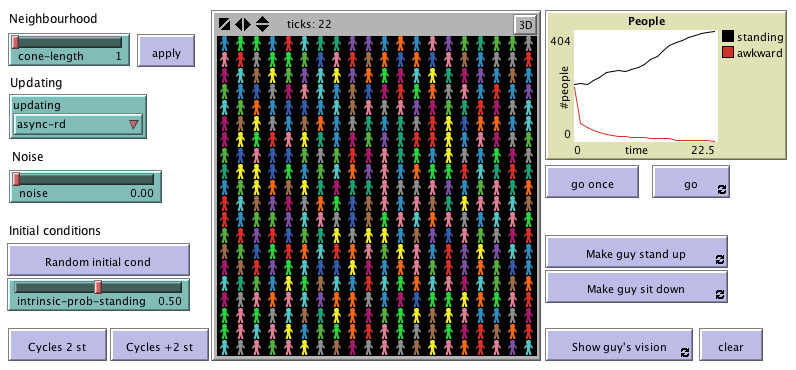
The state of the system can be defined by a vector s of dimension L2, containing the L2 agents' status: si = 1 if agent i is standing, and si = 0 if agent i is seated. Hence the state space is a finite set of 2L2 states. Note that any state can be observed because the initial quality qi perceived by each agent follows a uniform distribution (and the threshold value equals 0.5).
We start by proving that the system has only two absorbing states (everyone seated, and everyone standing) regardless of the value of L, the updating mechanism (SU or ARU) and the type of neighbourhood ("five neighbours" or "conical neighbourhood"). To see this, note that a state i is absorbing if and only if pi,i = 1. In other words, in an absorbing state every agent is in one of the following two situations:
The proof rests on the following facts:
In this section we demonstrate that the only two absorbing classes in the ARU model correspond to the two unique absorbing states described in the previous section. This can be proved by showing that it is possible to reach (at least) one absorbing state from any given state (and therefore we can assert that there isn't any closed communicating class with more than one state in the model) [2].
The proof goes as follows:
Thus, from any arbitrary state it is possible to reach (at least) one of the two absorbing states (everyone seated, or everyone standing) regardless of the value of L and the type of neighbourhood ("five neighbours" or "conical neighbourhood").
Having proved that the only two absorbing classes in the ARU model correspond to the two absorbing states, using Proposition 2 we can partition the state space as follows: S = {abs1} ∪ {abs2} ∪ T, where abs1 and abs2 are the two absorbing states (everyone standing, and everyone seated), and T is the union of all non-closed communicating classes. Taking into account Proposition 3 we can conclude that sooner or later the THMC will enter one of the two absorbing states and stay in it forever. Naturally, the probability of ending up in each of the two absorbing states depends on the initial conditions.
The same conclusions are valid for the third updating mechanism considered by Miller and Page (2004), called Asynchronous-Incentive-Based Updating. (See footnote 3.)
The analysis of the SU model is significantly different from that of the ARU model. With synchronous updating, all agents review their decision in unison. As demonstrated above, the SU model has only two absorbing states but, in contrast to the ARU model, in the SU model there can be many periodic recurrent classes. Some of these classes contain only 2 states (the reader may see several examples by pressing the button Cycles 2 st in Applet 1), and some others contain more than 2 states (the reader may see several examples by pressing the button Cycles +2 st in Applet 1) –depending on the type of neighbourhood–. As previously shown, all these periodic classes are not present in the ARU model.
Thus, in the SU model there are several absorbing classes and, naturally, the probability of ending up trapped in any particular one depends on the initial conditions.
In this section we present a slight variation of Miller and Page's (2004) model where each agent may change her status with a certain exogenous probability. To be precise, each individual agent, immediately after having revised her status, will change it to the opposite with probability noise: a standing agent will sit with probability noise, whereas a seated agent will stand up with probability noise.
Introducing noise changes the dynamics of the model significantly. It is clear that –regardless of the value of L, the updating mechanism (SU or ARU) and the type of neighbourhood ("five neighbours" or "conical neighbourhood")– the inclusion of noise prevents the system from locking in any state, i.e. there are no absorbing states anymore. As a matter of fact, the model with noise ∈ (0, 1) satisfies sufficient condition (i) for irreducibility and aperiodicity pointed out in Proposition 4 of our paper:
The demonstration of this statement is simple when one realises that the inclusion of noise guarantees that it is possible to go from any state to any other state in one single step. Consequently the model is an irreducible and aperiodic THMC, also called ergodic. As we have seen in the paper, in these processes the probability of finding the system in each of its states in the long run is strictly positive and independent of the initial conditions. Furthermore the limiting distribution π coincides with the occupancy distribution π*. Calculating such probabilities by deriving the transition matrix and its powers seems rather impractical, but we can approximate them as much as we want by running just one simulation for long enough.
Note that the conclusions provided in this section are independent of the initial conditions (i.e. independent of the quality of the performance), of the precise value of the noise (as long as it is in the interval (0, 1)), of the value of L, of the updating mechanism and of the type of neighbourhood.
As argued above, the ARU model with noise has no absorbing states anymore, but it is clear that the two Previously Absorbing States (PAS) are the only two stochastically stable states (see section 10 of our paper). The proof of this statement is straightforward once we realise that symmetric considerations imply that the two PAS are equivalent. Thus, in the limit as noise goes to zero, the limiting distribution π will concentrate on each of the PAS with probability 0.5. In other words, the only two states that would be observed with positive probability in the limit as noise tends to zero are the two PAS, and they would be observed with equal probability.
StandingOvation is an agent-based model described by Miller and Page in their paper:
Miller, J. H. and S. E. Page (2004). "The standing ovation problem" Complexity 9(5): 8-16.
Copyright (C) 2008 Luis R. Izquierdo, Segismundo S. Izquierdo, José M. Galán & José I. Santos
This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.
This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.
You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.
Contact information:
Luis R. Izquierdo
University of Burgos, Spain.
e-mail: lrizquierdo@ubu.es
This program has been designed and implemented by Luis R. Izquierdo, Segismundo S. Izquierdo, José M. Galán & José I. Santos
de MARCHI S (2005) Computational and Mathematical Modeling in the Social Sciences. Cambridge University Press.
MILLER J H & Page S E (2004) The Standing Ovation Problem. Complexity 9(5), pp. 8-16.
MILLER J H & Page S E (2007) Complex Adaptive Systems: An Introduction to Computational Models of Social Life. Princeton University Press.
WILENSKY U (1999). NetLogo. Evanston, IL Center for Connected Learning and Computer-Based Modeling, Northwestern University. http://ccl.northwestern.edu/netlogo/.
2 The method used here to prove that something is possible consists in identifying a sequence of random events that can occur with strictly positive probability.
3 Note that given any arbitrary state, there is a strictly positive probability that the agent located at the leftmost location in the first row and her only neighbour adopt the same status in the following state. From this second state, there is a strictly positive probability that the third agent adopts this same status while the previous two keep it. This reasoning can be continued for the following agents in the first row. Thus, after a number of time-steps, there is a strictly positive probability of reaching a state where every agent in the first row is in the same status. This situation necessarily leads to a situation where every agent in the auditorium adopts that same status.