Branching innovation, recombinant innovation, and endogenous technological transitions

Koen Frenken, Luis R. Izquierdo & Paolo Zeppini

HOW TO INSTALL THE MODEL

To use Recombranch, you will have to install NetLogo 5.3.1 (free and open source) and download the model itself. Unzip the downloaded file and click on recombranch.nlogo

OVERVIEW OF THE MODEL

Recombranch is an evolutionary model of technological transitions designed to explore the dynamics of innovation. The model is based on two different types of innovations: Branching innovations and recombinant innovations. Branching innovations refer to technological improvements along a particular path, while recombinant innovations represent fusions of multiple paths. Recombinant innovations create "short-cuts" which reduce switching costs allowing agents to escape a technological lock-in. As a result, recombinant innovations speed up technological progress allowing transitions that are impossible with only branching innovations.

The model replicates some stylised facts of technological change, such as technological lock-in, experimental failure, punctuated change and irreversibility. Furthermore, an extensive simulation experiment reported in Frenken, Izquierdo & Zeppini (2012) suggests that there is an optimal rate of innovation, which is strongly correlated with the number of recombination innovations. This underlines the pivotal role of technological variety as a seed for recombinant innovation leading to technological transitions.

DESCRIPTION OF THE MODEL

This section explains the formal model that Recombranch implements. The information provided here should suffice to re-implement the same formal model in any sophisticated enough modelling platform. We use bold red italicised arial font to denote parameters (i.e. variables that can be set by the user), and we use bold green italicised arial font to denote the name of the corresponding slider in the interface of the model above. All sliders can be changed at run-time with immediate effect on the dynamics of the model (except the number of agents in the run num-agents).

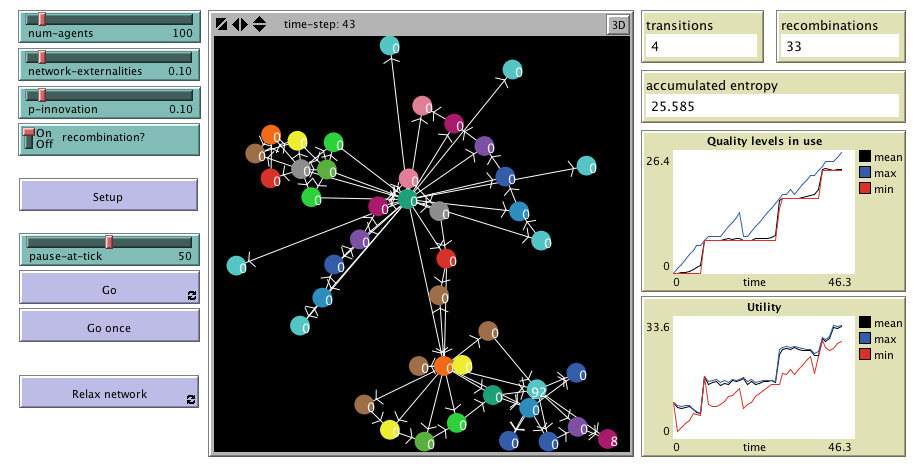
In the model there is a constant population of N agents (num-agents ≥ 1) and an evolving set of technologies that agents may use. The model runs in discrete time-steps. At any given time-step t, each agent is using one and only one technology, and derives a certain utility from doing so. The utility u_α,t gained at time-step t when using technology α comes from an intrinsic quality of the technology l_α and from the positive externalities that other users of technology α exercise on the considered agent:

u_α,t = l_α + e·n_α,t

where n_α,t indicates the number of agents using technology α in period t, and the parameter e ∈ [0,1] measures the strength of the externalities (network-externalities). Each time-step in the model consists of two stages that take place sequentially: the innovation stage and the decision stage.

Innovation stage

Technologies form a directed network where they represent the nodes, while the links express the genealogical relation. This network evolves in time due to the possibility that agents innovate and create new technologies. In every time-step, each individual agent innovates with independent probability p (p-innovation ∈ [0,1]). Innovations take place differently depending on whether recombinations of existing technologies are allowed or not, something which is determined exogenously in the model (using the switch recombination?).

• If recombinations are not allowed (i.e. recombination? is off), each group of innovators using the same technology α branch out from technology α to jointly create a new technology α* with intrinsic quality level l_α* = l_α + 1. Thus, in this case the number of technologies created in time-step t equals the number of different technologies being used by the innovators.
• If recombinations are allowed (i.e. recombination? is on), all innovators join up to create one single new technology β by recombining all the different technologies α_i they are currently using. The intrinsic quality level of the new technology is one unit higher than the highest quality of the technologies being recombined, i.e. l_β = max_i{l_αi} + 1.

In either case, whenever a new technology is created, a link is formed from each of the technologies used by its creators to the newly created technology. If all the creators of a new technology come from the same technology we say that the innovation occurred by branching. Otherwise we say that the innovation occurred by recombination. Thus, it is clear that a technology has been created by recombination if and only if it has more than one incoming link in the network.

Decision stage

The decision procedure is different depending on whether the agent innovated or not. Naturally, all time-step innovators decide to use the technology they just created. Then, the agents who have not innovated in the current time-step synchronously decide which technology to use. The non-innovating agents will switch to the technology that provides them with the highest utility, once switching costs are taken into account. We assume that the cost of switching from technology α to technology β equals the geodesic distance d_αβ between technologies α and β in the technological network. Thus, the benefit of switching from technology α to technology β is:

Δu_α→β,t = u_β,t - u_α,t - d_αβ

A non-innovating agent using technology α will change technology if and only if there exists some other technology β such that Δu_α→β,t > 0. In that case the agent will choose the technology that provides him with the highest benefit Δu_α→·,t. Ties are resolved randomly.

PARAMETERS AND BUTTONS

• num-agents (N): Number of agents in the run.
• network-externalities (e): Parameter that measures the strength of the externalities (u_α,t = l_α + e·n_α,t).
• p-innovation (p ∈ [0,1]): Probability with which each individual agent innovates in each time-step.
• recombination?: Switch (it can be either on or off) that determines whether recombinations are allowed or not.
• pause-at-tick: The model will halt at the end of this time-step. To resume, you can press the button Go again.

Buttons

• Setup: Creates one single initial technology with num-agents users.
• Go: Pressing this button will run the model until this same button is pressed again (or until time-step pause-at-time-step, if not reached yet).
• Go once: Pressing this button will run the model one time step only.
• Relax network: Pressing this button the network of technologies is laid out nicely so the network topology can be easily appreciated. This button has visual effects only

MONITORS AND PLOTS

Monitors

• time-step: Time-step in the model. The monitor is placed at the top of the black window.
• transitions: Number of transitions in the run. A transition occurs if and only if the minimum quality level l_α across agents (i.e. of every technology α in use) increases.
• recombinations: Number of recombinations in the run. We say that a technology has been created by recombination if and only if at least two of its creators were using different technologies before becoming innovators.
• accumulated entropy: Accumulated entropy since the beginning of the run. Entropy measures the variety of technologies that are in use. In a given time-step t, the entropy of the system is defined as: Entropy_t = - ∑_α(n_α,t/N)·log₂(n_α,t/N).

Plots

• Quality levels in use: Time series of the (minimum, maximum, and mean) quality levels of the technologies that are being used by at least one agent.
• Utility: Time series of the (minimum, maximum, and mean) utility obtained by the agents.

LICENCE

Recombranch is an evolutionary model of technological transitions designed to explore the dynamics of innovation.
Copyright (C) 2009 Koen Frenken, Luis R. Izquierdo & Paolo Zeppini.

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.

Contact information:
Luis R. Izquierdo
University of Burgos, Spain.
e-mail: lrizquierdo@ubu.es

MODELLERS

This program has been designed and implemented by Koen Frenken>Koen Frenken, Luis R. Izquierdo & Paolo Zeppini.

REFERENCES

• Koen FrenkenFrenken, K., Izquierdo, L.R. & Zeppini, P. (2012). Branching innovation, recombinant innovation, and endogenous technological transitions. Environmental Innovation and Societal Transitions. [Download]