nBEPA1 in Single-optimum Coordination Games

Luis R. Izquierdo & Segismundo S. Izquierdo

HOW TO INSTALL THE MODEL

To use nBEPA1-SOCG (protocol noisy Best Experienced Payoff, test All, 1 trial, in Single Optimum Coordination Games), you will have to install NetLogo 6.2.1 (free and open source) and download the model itself. Unzip the downloaded file and click on nbepa1-socg.nlogo

DESCRIPTION OF THE MODEL

This section explains the formal model that nBEPA1-SOCG implements. The information provided here should suffice to re-implement the same formal model in any sophisticated enough modelling platform. We use bold green italicised arial font to denote parameters (i.e. variables that can be set by the user).

Population

In the model, there is a population of \(N\) agents who repeatedly play a Single-Optimum Coordination Game in pairs.

The Game

The Single-Optimum Coordination Game is a 2-player \(n\)-strategy game with the following payoff matrix: \[ \left(\begin{array}{ccccc} 1&0&0&...&0\\ 0&2&0&...&0\\ 0&0&\ddots&&\vdots\\ \vdots&\vdots&&n-1&0\\ 0&0&...&0&n\\ \end{array} \right) \]

Note that the optimal outcome is achieved if both players choose strategy \(n\).

The nBEPA1 revision protocol

From time to time, agents are given the opportunity to revise their strategy, and they do so following the nBEPA1 revision protocol:

• With probability noise, the revising agent chooses one of the \(n\) strategies at random.
• With probability (1-noise), the revising agent tests each of the \(n\) strategies, by playing each of them once. Crucially, the revising agent tries each one of its strategies against a randomly drawn opponent; thus, each trial is conducted with a potentially different counterpart. Once each of the \(n\) strategies has been tried against one (potentially different) opponent, the revising agent chooses the strategy that provided the greatest payoff in the test, resolving the possible ties at random.

Sequence of events

Initially, agents are assigned a strategy according to the initial distribution n-of-players-for-each-strategy = \(\left[a_1, a_2, ..., a_n\right]\) set by the user, where \(a_i\) denotes the number of agents using strategy \(i\). The population size \(N\) and the number of strategies \(n\) in the game are computed from the initial distribution, since \(N = \sum_i a_i\) and \(n\) is the number of elements in the initial distribution.

The model then runs in discrete time-steps called ticks. Within each tick, agents are given the opportunity to revise their strategies. The way agents are scheduled to revise their strategies is specified by the user with parameter updating, which can take three values:

• Asynchronous random independent. In every tick, we repeat the following procedure as many times as agents there are: "Take one agent at random and give it the opportunity to revise its strategy."
• Asynchronous random order. In every tick, we give all agents the opportunity to revise their strategy sequentially in a random order.
• Synchronous. In every tick, all agents revise their strategy at the same time (i.e. synchronously).

Note that, in every tick, exactly \(N\) revisions take place regardless of the value of updating. This sequence of events is repeated iteratively.

HOW TO USE IT

Parameters

• n-of-players-for-each-strategy: List of the form \(\left[a_1, a_2, ..., a_n\right]\), where \(a_i\) denotes the initial number of agents using strategy \(i\).
• updating: Updating scheme used to conduct the revisions. It can take the following three values:
  • Asynchronous random independent
  • Asynchronous random order
  • Synchronous
  The value of this parameter can be changed at runtime, with immediate effect on the run.
• noise: Probability of experimentation, i.e. probability with which a revising agent adopts a random strategy. The value of this parameter can be changed at runtime, with immediate effect on the run.

Buttons

• setup: Sets the model up, creating a population of agents with initial strategies determined by parameter n-of-players-for-each-strategy.
• go once: Pressing this button will run the model one tick only.
• go: Pressing this button will run the model until this same button is pressed again.

MONITOR, TEXT BOX AND PLOT

• ticks: Number of ticks that have gone by.
• Payoff matrix: Text box showing the payoff matrix of the single-optimum coordination game being played. The game has as many strategies as elements there are in n-of-players-for-each-strategy.
• Strategy distribution: Time series of the distribution of strategies in the population.

LICENCE

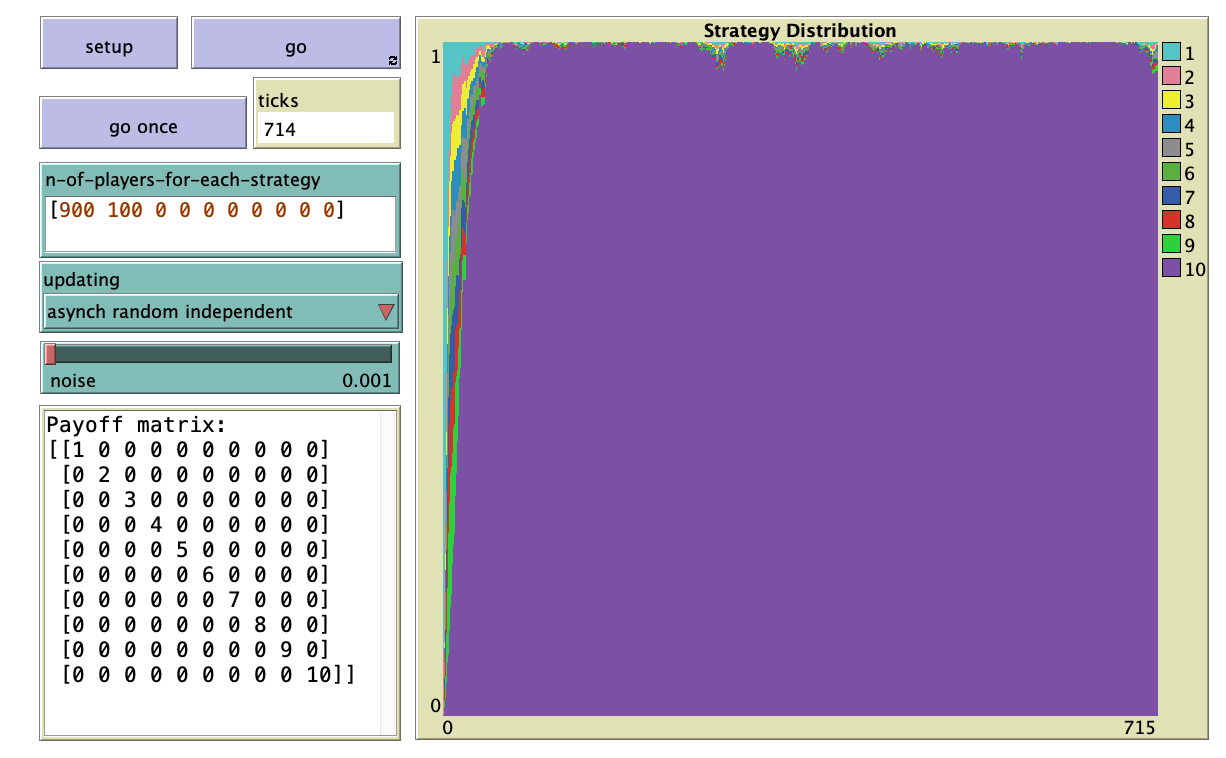
nbepa1-socg is a NetLogo model designed to analyze the nBEPA1 (noisy Best Experienced Payoff, test All, 1 trial) protocol in Single Optimum Coordination Games.
Copyright (C) 2021 Luis R. Izquierdo & Segismundo S. Izquierdo

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.

Contact information:
Luis R. Izquierdo
University of Burgos, Spain.
e-mail: lrizquierdo@ubu.es

MODELLERS

This program has been designed and implemented by Luis R. Izquierdo & Segismundo S. Izquierdo.

REFERENCES

Izquierdo, L. R., Izquierdo, S. S. and Rodríguez, J. (2021). Fast and Scalable Global Convergence in Single-Optimum Decentralized Coordination Problems. Working paper.