Agent-Based Evolutionary Dynamics in 2 populations

Abed-2pop is a modeling framework designed to simulate the evolution of two populations of agents who play a 2-player game. Agents in one population play the game with agents in the other population. Every agent is occasionally given the opportunity to revise his strategy.

How to install Abed-2pop

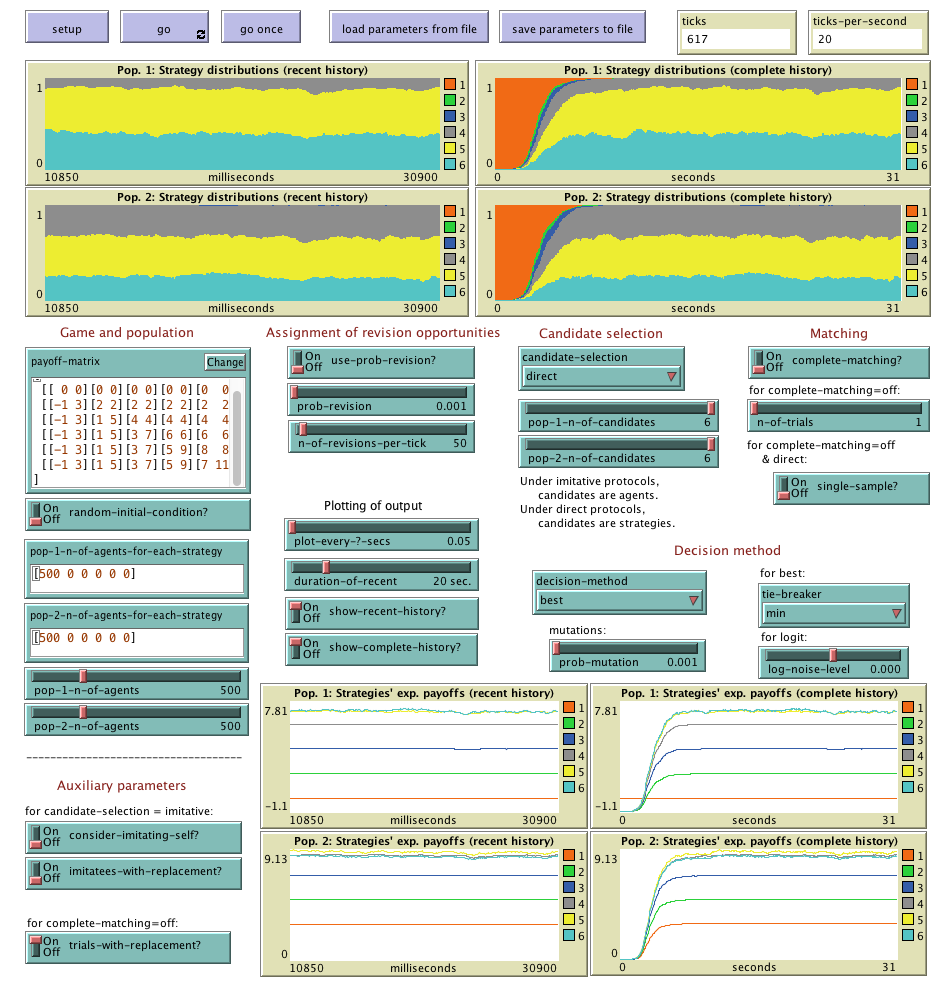
To use Abed-2pop, you will have to install NetLogo (free and open source) 6.0.1 or higher and download this zip file. The zip file contains the model itself (abed-2pop.nlogo) and also this very webpage (which contains a description of the model). To run the model, you just have to click on the file abed-2pop.nlogo. The figure below shows Abed-2pop's interface.

Overview

We use bold green fonts to denote parameters (i.e. variables that can be set by the user) and brown fonts to denote different values that a parameter might take.

Abed-2pop is a modeling framework designed to simulate the evolution of two populations of agents who recurrently play a 2-player game defined by a payoff-matrix. Agents in population 1 adopt the role of the row player in the game, whilst those in population 2 adopt the role of the column player. Agents use pure strategies only, and they occasionally revise their strategy.

The simulation runs in discrete time-steps called ticks. Within each tick:

The set of revising agents is chosen
The game is played by the revising agents and all the agents involved in their revision
The revising agents simultaneously update their strategies

This sequence of events, which is explained below in detail, is repetead iteratively.

Selection of revising agents

All agents are equally likely to revise their strategy in every tick. There are two ways in which the set of revising agents can be chosen:

By setting parameter prob-revision, which is the probability that each individual agent revises his strategy in every tick.
By setting parameter n-of-revisions-per-tick, which is the number of randomly selected agents that will revise their strategy in every tick. These agents are selected without taking into account the population they belong to.

Computation of payoffs

The payoff that each agent obtains in each tick is computed as the average payoff over n-of-trials matches (where the agent uses his particular pure strategy, and his -randomly chosen- counterparts from the other population theirs).

Note that two agents using the same strategy may get different payoffs because they may encounter different counterparts in their trials.

Specifying how payoffs are computed

There are parameters to specify:

the n-of-trials agents make, and
whether these are conducted with or without replacement ( trials-with-replacement? ).

Strategy revision

Agents are occasionally given the opportunity to revise their strategy. The specific protocol used by revising agents is determined mainly by the following parameters:

candidate-selection, which indicates whether the protocol is imitative or direct (Sandholm, 2010, p. 9),
pop-i-n-of-candidates, which determine the number of candidates (agents or strategies) that revising agents in population i will consider to update their strategy, and
decision-method, which determines how to single out one instance out of the set of candidates. Abed-2pop implements the following methods: best, logit, positive-proportional, pairwise-difference, linear-dissatisfaction and linear-attraction.

We briefly explain the meaning of each of these terms below.

Imitative Protocols

Under imitative protocols, revising agents observe what other agents in the same population are doing and their payoff, and use this information to update their strategy. Specifically, revising agents in population i will compile a multiset of pop-i-n-of-candidates agents in their same population to copy the strategy of one of them. The revising agent is always part of this multiset of agents. The selection of the other ( pop-i-n-of-candidates - 1 ) agents is conducted randomly, so popular strategies in the population are more likely to be observed than less popular ones. Once the multiset of candidate agents has been compiled, the revising agent will use one of various possible decision-methods (see below) to single out one of the candidates and copy his strategy.

Imitative protocols: Specifying how to compile the set of candidate agents to copy

There are parameters to specify:

the number of candidate agents that revising agents will consider to copy ( pop-1-n-of-candidates and pop-2-n-of-candidates ),
whether the selection of other candidates (besides the revising agent) is conducted with or without replacement ( imitatees-with-replacement? ), and
whether the selection of other candidates (besides the revising agent) considers the revising agent again or not ( consider-imitating-self? ).

Direct Protocols

In contrast, under direct protocols, revising agents choose candidate strategies directly, so a strategy's popularity does not directly influence the probability with which it is considered. Specifically, a revising agent in population i considers a set of pop-i-n-of-candidates strategies (including his own), tests them, and selects one of them according to one of various possible decision-methods (see below).

Direct protocols: Specifying how to test strategies

There are parameters to specify:

the number of strategies that revising agents consider, including their current strategy ( pop-1-n-of-candidates and pop-2-n-of-candidates ),
whether the strategies in the test set are compared according to a payoff computed using one single sample of counterparts from the other population (i.e. the same set of counterparts for every strategy), or whether the payoff of each strategy in the test set is computed using a freshly drawn random sample of counterparts ( single-sample? ).

Decision methods

A decision-method is a procedure that singles out:

one particular agent out of a set of candidates, whose strategy will be adopted by the revising agent (in imitative protocols), or
one particular strategy out of a set of candidate strategies, which will be adopted by the revising agent (in direct protocols).

The selection is based on the (average) payoff obtained by each of the candidates (agents or strategies) in the input set. In imitative protocols the set of candidates is the multiset of ( pop-1-n-of-candidates or pop-2-n-of-candidates ) agents previously compiled, which always includes the revising agent. In direct protocols the set of candidates is the set of ( pop-1-n-of-candidates or pop-2-n-of-candidates ) strategies previously compiled, which always includes the revising agent's strategy. Abed-2pop implements six different decision-methods:

best: The candidate with the highest payoff is selected. Ties are resolved according to the procedure indicated with parameter tie-breaker.
logit: A random weighted choice is conducted among the candidates. The weight for each candidate is e^{(payoff / (10 ^ log-noise-level))}.
positive-proportional: A candidate is randomly selected with probabilities proportional to payoffs. Thus, payoffs should be non-negative if this decision-method is used.
pairwise-difference: In this method the set of candidates contains two elements only: the one corresponding to the revising agent's own strategy (or to himself in imitative protocols) and another one. The revising agent adopts the other candidate strategy only if the other candidate's payoff is higher than his own, and he does so with probability proportional to the payoff difference.
linear-dissatisfaction: In this method the set of candidates contains two elements only: the one corresponding to the revising agent's own strategy (or to himself in imitative protocols) and another one. The revising agent adopts the other candidate strategy with probability proportional to the difference between the maximum possible payoff he could get and his own payoff. (The other candidate's payoff is ignored.)
linear-attraction: In this method the set of candidates contains two elements only: the one corresponding to the revising agent's own strategy (or to himself in imitative protocols) and another one. The revising agent adopts the other candidate strategy with probability proportional to the difference between the other candidate's payoff and the minimum possible payoff he could get. (The revising agent's payoff is ignored.)

Parameters

Parameters to set up the population and its initial strategy distribution

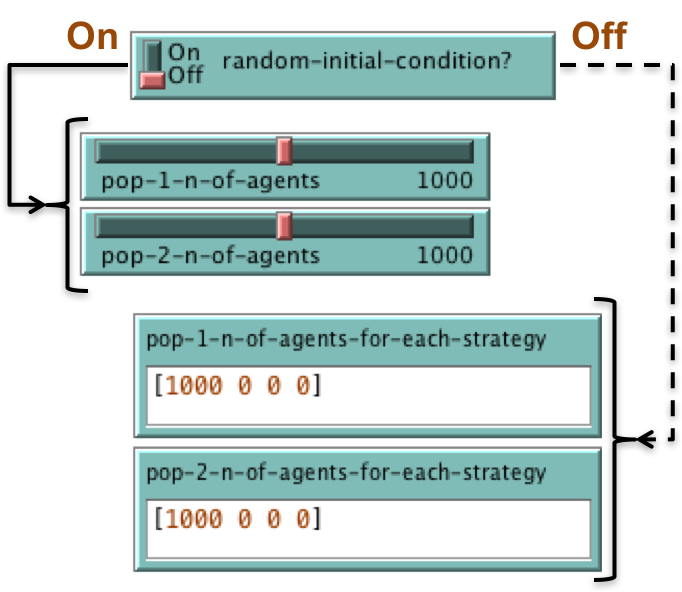
If random-initial-condition? is On, population 1 will consist of pop-1-n-of-agents agents and population 2 will consist of pop-2-n-of-agents agents, each of them with a random initial strategy.
If random-initial-condition? is Off, population i will be created from the list given as pop-i-n-of-agents-for-each-strategy. Let this list be [x1 x2 ... xn]; then the initial population will consist of x1 agents playing strategy 1, x2 agents playing strategy 2, ... , and xn agents playing strategy n. The value of pop-i-n-of-agents is then set to the total number of agents in the population.

The value of pop-i-n-of-agents can be changed at runtime with immediate effect over the model. If pop-i-n-of-agents is reduced, the necessary number of (randomly selected) agents are killed. If pop-i-n-of-agents is increased, the necessary number of (randomly selected) agents are cloned.

Parameters that determine when agents revise their strategy

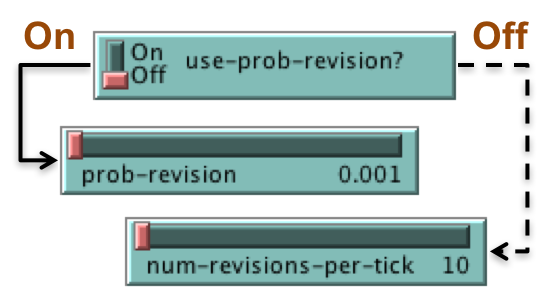
If use-prob-revision? is On, each individual agent revises his strategy with probability prob-revision in every tick.
If use-prob-revision? is Off, then n-of-revisions-per-tick agents are randomly selected to revise their strategy in every tick. These agents are selected without taking into account the population they belong to.

The value of these three parameters can be changed at runtime with immediate effect on the model.

Parameters that determine how payoffs are calculated

This flowchart is a summary of all the parameters that determine how payoffs are calculated.

The idea is to start at the top of the flowchart, give a value to every parameter you encounter on your way and, at the decision nodes (i.e. the red diamonds), select the exit arrow whose [label] indicates the value of the parameter you have just chosen. Thus, note that, depending on your choices, it may not be necessary to set the value of all parameters.

Every parameter is explained below.

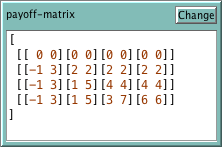
Payoff matrix for the 2-player game. Entry A_ij in the matrix is a 2-element list [p1 p2] which refers to the outcome where player row chooses strategy i and player column uses strategy j. Within the list [p1 p2], p1 denotes the payoff obtained by player row (in population 1) and p2 denotes the payoff obtained by player column (in population 2). The number of strategies for agents in population 1 (population 2) is assumed to be the number of rows (columns) in this payoff matrix.

If complete-matching? is On, payoffs are calculated assuming that every agent in each population plays with every agent in the other population.

If complete-matching? is Off, then parameters n-of-trials, trials-with-replacement? and single-sample? become relevant.

Parameter n-of-trials indicates the number of matches over which payoffs are computed. The user can set the value of this parameter only if complete-matching? is Off.

Parameter trials-with-replacement? indicates whether the sample of counterparts used to compute payoffs is taken with replacement ( On ) or without replacement ( Off ). The user can set the value of this parameter only if complete-matching? is Off.

Parameters that determine how agents revise their strategy

With probability prob-mutation the revising agent will select a random strategy. With probability (1 - prob-mutation) he will revise his strategy following an algorithm which is mainly determined by the parameters shown in the flowchart below.

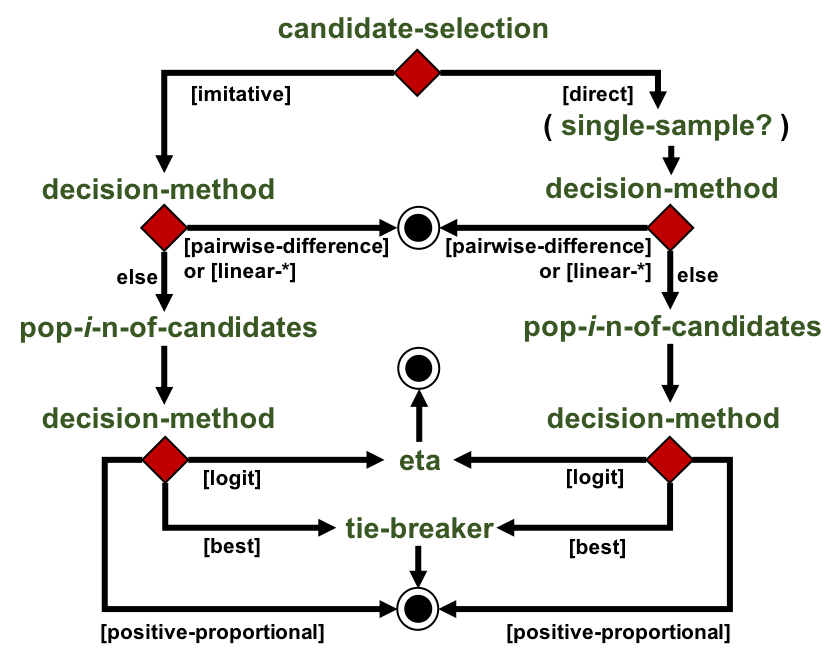
Parameter candidate-selection indicates whether the protocol is imitative or direct (Sandholm, 2010, p. 9). Revising agents compile a multiset of candidate agents to imitate to (in imitative protocols) or a set of candidate strategies they will consider adopting (in direct protocols). The following describes how the multiset of candidates is formed.

imitative
direct

The multiset of candidate agents contains the revising agent (which is always included) plus a sample of ( pop-i-n-of-candidates - 1 ) elements from his population. Two parameters determine how this sample is taken:

imitatees-with-replacement? indicates whether the sample is taken with or without replacement.
consider-imitating-self? indicates whether the sample is taken from the revising agent's whole population (i.e. including the reviser) or from the revising agent's whole population excluding the reviser. Note that, in any case, the reviser is always part of the multiset of candidate agents at least once.

To be sure, let Sample(n, p, R) denote a sample of n = ( pop-i-n-of-candidates - 1 ) elements from population p with replacement. Similarly, let Sample(n, p, NR) denote the same sampling procedure, but without replacement. Finally, let P denote the revising agent's whole population. Using this notation, the multiset of candidate agents will be formed by

reviser + Sample(n, P, R) ; if imitatees-with-replacement? = On and consider-imitating-self? = On.

reviser + Sample(n, P, NR) ; if imitatees-with-replacement? = Off and consider-imitating-self? = On.

reviser + Sample(n, P - reviser, R) ; if imitatees-with-replacement? = On and consider-imitating-self? = Off.

reviser + Sample(n, P - reviser, NR) ; if imitatees-with-replacement? = Off and consider-imitating-self? = Off.

The set of candidate strategies contains the revising agent's own strategy plus ( pop-i-n-of-candidates - 1 ) other strategies, selected at random.

Parameter single-sample? is only relevant in direct protocols (i.e. if candidate-selection is direct). It indicates whether strategies being compared are tested against one single sample of agents (i.e. the same set of agents for every strategy), or whether the payoff of each strategy in the test-set is computed using a freshly drawn random sample of agents.

The user can set the value of this parameter only if complete-matching? is Off.

Parameter decision-method determines which strategy the revising agent will adopt.

Specifically, the chosen decision-method (i.e. best, logit, positive-proportional, pairwise-difference, linear-dissatisfaction or linear-attraction) selects one particular instance from the set of candidates previously compiled, based on the payoff obtained by each of the candidates. The revising agent will then adopt the strategy of the selected candidate.

The candidate with the highest payoff is returned. Ties are resolved using the selected tie-breaker. Possible values of tie-breaker are:

stick-uniform: If the current strategy of the revising agent is in the tie, the revising agent sticks to it. Otherwise, a random choice is made using the uniform distribution.
stick-min: If the current strategy of the revising agent is in the tie, the revising agent sticks to it. Otherwise, the strategy with the minimum number is selected.
uniform: A random choice is made using the uniform distribution.
min: The strategy with the minimum number is selected.
random-walk: This tie-breaker makes use of an auxiliary random walk (one for each population) that is running in the background. Let N be the number of agents in the population and let n be the number of strategies. In the auxiliary random walk, there are N rw-agents, plus a set of n so-called committed rw-agents, one for each of the n strategies in the population. The committed rw-agents never change strategy. In each iteration of this random walk, one uncommitted rw-agent is selected at random to imitate another (committed or uncommitted) rw-agent, also chosen at random. We run one iteration of this process per tick. When there is a tie, the relative frequency of each strategy in the corresponding auxiliary random walk is used as a weight to make a random weighted selection among the tied candidates.

The random-walk tie-breaker is inspired by section 11.4.3 in Sandholm (2010, pp. 421-423).

A random weighted choice is conducted among the candidates. The weight for each candidate is e^{(payoff / (10 ^ log-noise-level))}.

If log-noise-level is large, choices under logit are nearly uniform. If log-noise-level is small (i.e. negative and large in magnitude), choices resemble those made by best, at least when the difference between the best and the second-best payoff is not too small (Sandholm, 2010, p. 128 & pp. 191-6).

A candidate is randomly selected, with probabilities proportional to payoffs. Because of this, when using positive-proportional, payoffs should not be negative. Recall that the payoff for each candidate is the average payoff over the n-of-trials matches.

In pairwise-difference, the agent always considers exactly two candidates (one corresponding to his own strategy or to himself, and another one), i.e., the value of pop-i-n-of-candidates is automatically set to 2.

The revising agent will consider adopting the other candidate strategy only if the other candidate's payoff is higher than his own, and he will actually adopt it with probability proportional to the payoff difference. In order to turn the difference in payoffs into a meaningful probability, we divide the payoff difference by the maximum possible payoff difference that could occur in that population (i.e. the maximum payoff an agent in that role could ever get minus the minimum payoff he could ever obtain).

If complete-matching? is On, the mean dynamics for large populations of the imitative pairwise-difference protocol (sometimes called pairwise proportional imitation) is the replicator dynamics up to a speed factor (see Sandholm, 2010, pp. 126-7).

In linear-dissatisfaction, the agent always considers exactly two candidates (one corresponding to his own strategy or to himself, and another one), i.e., the value of n-of-candidates is automatically set to 2.

The revising agent will adopt the other candidate strategy with probability equal to the difference between the maximum possible payoff that someone could get in that population and his own payoff, divided by the maximum possible payoff minus the minimum possible payoff (which someone could get in that population). (The other candidate's payoff is ignored.)

In linear-attraction, the agent always considers exactly two candidates (one corresponding to his own strategy or to himself, and another one), i.e., the value of n-of-candidates is automatically set to 2.

The revising agent will adopt the other candidate strategy with probability equal to the difference between the other candidate's payoff and the minimum possible payoff that someone could get in that population, divided by the maximum possible payoff minus the minimum possible payoff (which someone could get in that population). (The revising agent's payoff is ignored.)

How to save and load parameter files

Clicking on the button labeled , a window pops up to allow the user to save all parameter values in a .csv file.

Clicking on the button labeled , a window pops up to allow the user to load a parameter file in the same format as it is saved by Abed-2pop.

How to use it

Running the model

Once the model is parameterized (see Parameters section), click on the button labeled to initialize everything. Then, click on to run the model indefinitely (until you click on again). A click on runs the model one tick only.

The value of all parameters can be changed at runtime with immediate effect on the model

Plots and monitors

All plots in Abed-2pop show units of time in the horizontal axis. These are called seconds and milliseconds for simplicity, but they could be called "time units". One second is defined as the number of ticks over which the expected number of revisions equals the total number of agents (in both populations). This number of ticks is called and is shown in a monitor. The other monitor in Abed-2pop shows the that have been executed. Plots are updated every plot-every-?-secs seconds.

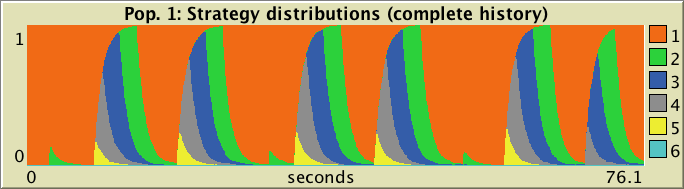
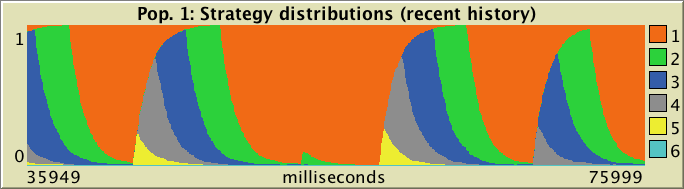
For each population, there are two plots to show the strategy distribution of agents as ticks go by, like the ones below:

complete-shares-pop-1

recent-shares-pop-1

and two other plots to show the expected payoff of each strategy as ticks go by, like the ones below:

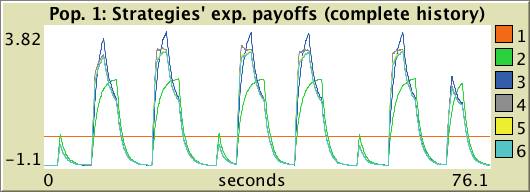
complete-payoffs-pop-1

recent-payoffs-pop-1

As you can see in the figures above, plots comes in two different flavors: one that shows the data from the beginning of the simulation (labeled complete history and active if show-complete-history? is On) and one that shows only the duration-of-recent last seconds in the simulation (labeled recent history and active if show-recent-history? is On).

License

Abed-2pop (Agent-Based Evolutionary Dynamics in 2 populations) is a modeling framework designed to simulate the evolution of two populations of agents who play a 2-player game. Agents in one population play the game with agents in the other population. Every agent is occasionally given the opportunity to revise his strategy.

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.

Contact information:
Luis R. Izquierdo
University of Burgos, Spain.
e-mail: lrizquierdo@ubu.es

Extending the model

You are most welcome to extend the model as you please, either privately or by creating a branch in our Github repository. If you’d like to see any specific feature implemented but you don’t know how to go about it, do feel free to email us and we’ll do our best to make it happen.

Acknowledgements

Financial support from the U.S. National Science Foundation, the U.S. Army Research Office, the Spanish Ministry of Economy and Competitiveness, and the Spanish Ministry of Science and Innovation is gratefully acknowledged.

References

Sandholm, W. H. (2010). Population Games and Evolutionary Dynamics. MIT Press, Cambridge.

How to cite

Izquierdo, L.R., Izquierdo, S.S. & Sandholm, W.H. (2019). An Introduction to ABED: Agent-Based Simulation of Evolutionary Game Dynamics. Games and Economic Behavior, 118, pp. 434-462.

[Download at publishers's site] | [Working Paper] | [Online appendix] | [Presentation]