ES-1-outcome (Endogenous Separation conditioned on the previous outcome)

Luis R. Izquierdo, Segismundo S. Izquierdo & Robert Boyd

HOW TO INSTALL THE MODEL

To use ES-1-outcome, you will have to install NetLogo 6.4 (free and open source) and download the model itself. Unzip the downloaded file and click on ES-1-outcome.nlogo

OVERVIEW OF THE MODEL

ES-1-outcome (Endogenous Separation conditioned on the previous outcome) is a model designed to formally analyze the mechanism of endogenous separation (or conditional dissociation) in the evolutionary emergence of cooperation. This section gives an informal and brief overview of ES-1-outcome. The figure below provides a sketch that illustrates the sequence of events within each time-step.

Sketch of the sequence of events within each time-step. The "Remaining Pairs" and "Singles" at the end of a time-step are identical to the "Existing Pairs" and "Singles" in the next time-step.

We use bold red italicised Arial font to denote parameters (i.e. variables that can be set by the user). In ES-1-outcome, there is a population of n-of-players players that are matched in couples (partnerships) to play a 2×2 symmetric game. The 2 possible actions players can take in the game are denoted C (for Cooperate) and D (for Defect).

After having played the game, partnerships may dissolve in two ways:

• Exogenously - a partnership is exogenously broken with probability (1-1/exp-n-of-interactions). Players who undergo exogenous separation revise their strategy with probability prob-revision.
• Endogenously - after observing the outcome of the game, either player may unilaterally choose to leave the partnership, according to their individual strategy.

Players who separate are randomly re-matched in the following period and continue playing the stage game with their new partner.

The model can be used to simulate processes with endogenous separation (if option-to-leave? = on) and processes without endogenous separation (if option-to-leave? = off).

DESCRIPTION OF THE MODEL

This section explains the formal model that ES-1-outcome implements. The information provided here should suffice to re-implement the same formal model in any sophisticated enough modelling platform.

The game

Consider a population of n-of-players individuals; some of the individuals are matched in pairs and some may be single.

Every individual who is single at the beginning of the time-step is randomly matched with another single. Thus, after this random matching of singles, every individual is paired with another individual.

In each time-step, the two members of every pair play a symmetric 2×2 game once, where each of them can undertake one of two possible actions. These two possible actions are called C (for Cooperate) and D (for Defect). The action selected by each of the players determines the payoff that each of them receives in that time-step: CC-payoff, CD-payoff, DC-payoff, or DD-payoff, where AB-payoff denotes the payoff that an individual choosing action A obtains when her counterpart chooses action B.

Memory-one strategies

Each individual carries five "genes" that shape her behaviour. These five genes determine the individual's strategy.

• First action: The first gene determines the individual's first action, i.e. the action (C or D) when the individual interacts with her partner for the very first time.
• After CC: The second gene determines what to do when the outcome of the interaction has been CC, i.e. both players have played C. The options are:
  • C: Stay with the current partner and, assuming the partnership continues, play C in the following time-step.
  • D: Stay with the current partner and, assuming the partnership continues, play D in the following time-step.
  • L: Leave the current partnership. In this case, the partnership is broken regardless of the decision of the partner.
• After CD: The third gene determines the choice -also C, D or L- after outcome CD, which denotes the situation where the individual has played C and the partner has played D.
• After DC: The fourth gene determines the choice (C, D or L) after outcome DC, which denotes the situation where the individual has played D and the partner has played C.
• After DD: Finally, the fifth gene determines the choice (C, D or L) after outcome DD, i.e. when the two players have defected.

A strategy thus specifies a course of action at every possible juncture in an individual's life. The number of possible memory-one strategies in the model with the option to leave (i.e., if option-to-leave? = on) is 2·3·3·3·3 = 162. The memory-one strategies for the model without the option to leave (option-to-leave? = off) are the 2·2⁴ = 32 strategies with no L.

We use these five genes to name the different strategies. An example of a strategy is D-C-L-D-C. A player with this strategy:

• Starts by playing D whenever the player meets a new partner.
• After CC, the player stays and plays C in the next interaction.
• After CD, the player leaves (L) the current partnership, so the two members of the partnership will join the pool of singles.
• After DC, the player stays and plays D in the next interaction.
• After DD, the player stays and plays C in the next interaction.

Thus, Tit-For-Tat corresponds to C-C-D-C-D, Win-Stay-Lose-Shift is C-C-D-D-C, and C-C-D-D-D is a strategy that chooses to cooperate with new partners and keeps on cooperating if and only if there is mutual cooperation; otherwise it defects.

Errors

There is also the possibility of errors when playing the game. Every time an individual must decide what action to take in the game (C or D), she will make an error (i.e. choose the unintended action) with probability action-error. Thus, the agent will take the action prescribed by her strategy with probability (1 - action-error) and the other one (C or D), with probability action-error:

The time line

The population process advances in discrete time-steps t = 1, 2, 3,... which are called 'ticks' in the interface of the model. In each time-step, the following events occur in sequence (see figure above):

1. Random matching of singles. At the beginning of each time-step, single individuals are randomly matched. Note that all individuals are single at the beginning of the very first time-step.
2. The stage game. All pairs play the 2×2 symmetric game described above once and obtain the corresponding payoff. Each individual's action (C or D) is determined by (the corresponding gene in) her strategy, potentially affected by action-error.
3. Exogenous separation. Every partnership is exogenously broken with probability (1-1/exp-n-of-interactions). Thus, parameter exp-n-of-interactions is the expected number of interactions of partnerships whose members do not choose to break up. If a partnership is broken, both players join the pool of singles.
4. Revision of strategies. Players whose partnership has been exogenously broken may revise their strategy, with independent probability prob-revision. The revision process is as follows:
   • With probability prob-experimentation, the revising player adopts a neighboring strategy within the set of feasible strategies. Two strategies are neighbors if and only they differ in exactly one gene. To be precise, revising players change one of the 5 genes that make up their strategy, chosen uniformly at random. Then,
     • If option-to-leave? = off, the action prescribed by the randomly chosen gene is flipped (C ↦ D, and D ↦ C).
     • If option-to-leave? = on, and the first gene is selected, the action prescribed is flipped (C ↦ D, and D ↦ C). If any of the other four genes is selected, then the action is replaced by any of the other two possibilities (C ↦ {D or L}, D ↦ {C or L}, and L ↦ {C or D}), with 50% probability of choosing each of them.
   • With probability (1-prob-experimentation), revising players choose one of the strategies that is being played in the population, with probability proportional to the total payoff obtained by the players using that strategy during the current stage. Izquierdo et al. (2024, Appendix A1) show three different ways one can implement this procedure.
5. Endogenous separation. Every individual involved in a partnership decides whether to leave or stay, according to her strategy. Individuals involved in partnerships that are broken join the pool of singles entering the next time-step.

HOW TO USE IT

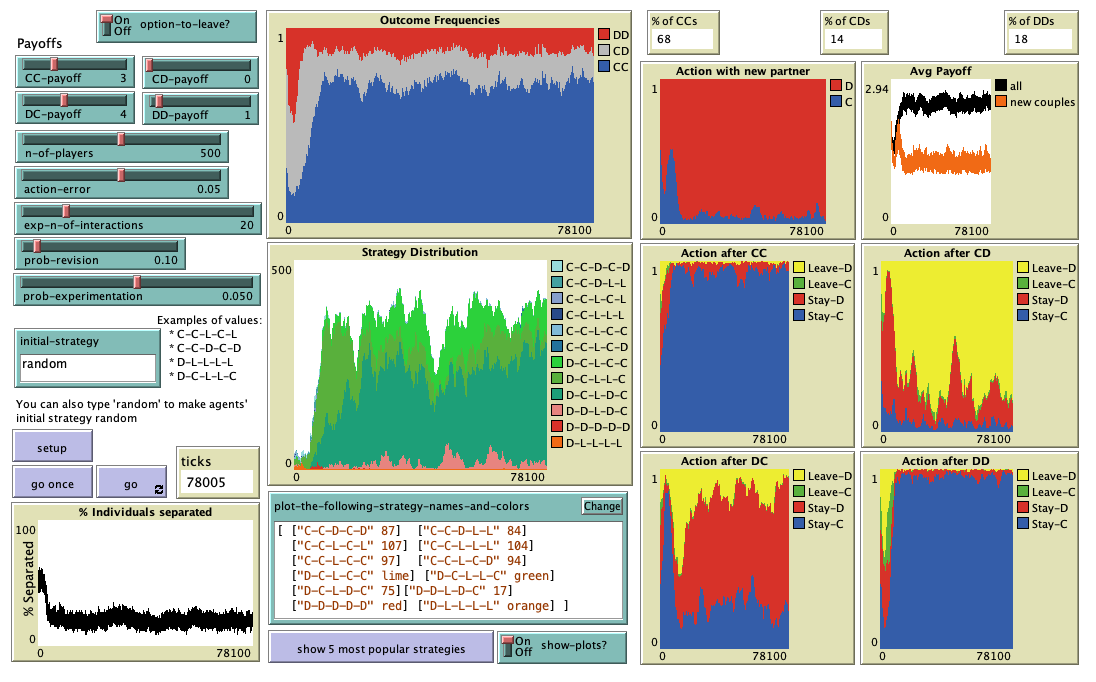
Type of model: with or without the option to leave

The user can choose to simulate a) a process with the option to leave (162 possible strategies), by setting option-to-leave? = on, or b) a process without that possibility (32 possible strategies), by turning option-to-leave? off.

Payoffs

• CC-payoff: Payoff obtained by a player who cooperates when the other player cooperates too.
• CD-payoff: Payoff obtained by a player who cooperates when the other player defects.
• DC-payoff: Payoff obtained by a player who defects when the other player cooperates.
• DD-payoff: Payoff obtained by a player who defects when the other player also defects.

Population parameters

• n-of-players: Number of players in the population
• action-error: Probability with which an individual makes an error when choosing the action in the game (C or D).
• exp-n-of-interactions: The expected number of interactions of partnerships whose members do not choose to break up. This actually sets the probability of exogenous breakup for each partnership at every time-step to the value 1/exp-n-of-interactions.
• prob-revision: Probability with which a player whose partnership has been exogenously broken revises her strategy.
• prob-experimentation: Probability with which a revising player adopts a random neighboring strategy within the set of feasible strategies.
• initial-strategy: Initial strategy for the population. It can be any of the 162 strategies for the whole population, or random.
  • If initial-strategy = random, each player takes one of the possible strategies with equal probability. There are 162 possible strategies if option-to-leave? = on and 32 if option-to-leave? = off.
  • Otherwise, every player in the population adopts the strategy introduced in this input box. To denote strategies, we use the notation X1-X2-X3-X4-X5, where:
    • X1 ∈ {C, D} is the action to take with a new partner,
    • X2 ∈ {C,D L} is the action to take after outcome CC,
    • X3 ∈ {C,D L} is the action to take after outcome CD,
    • X4 ∈ {C,D L} is the action to take after outcome DC,
    • X5 ∈ {C,D L} is the action to take after outcome DD,
    For instance, C-C-L-C-L is the strategy that always cooperates, stays (and cooperates) if the current partner cooperated in the previous interaction, and leaves if the partner defected in the previous interaction. C-C-D-C-D is the famous 'Tit for Tat'.

Buttons

• setup: Creates a new population of n-of-players players according to initial-strategy.
• go once: Pressing this button will run the model one time-step only.
• go: Pressing this button will run the model until this same button is pressed again.

• show 5 most popular strategies: When you press this button, a list is shown in the command center, with the 5 most popular strategies and the number of individuals that are using each of them.

MONITORS AND PLOTS

Monitors

• ticks: Number of time-steps that have gone by.

• % of CCs: Percentage of couples where both players cooperated in the current time-step.
• % of CDs: Percentage of couples where one player cooperated and the other player defected in the current time-step.
• % of DDs: Percentage of couples where both players defected in the current time-step.

Plots

Switch show-plots? controls whether plots are updated every tick or not. The model runs significantly faster if show-plots? is off. Importantly, all plots refer to the situation after the processes of exogenous and endogenous breakup have taken place but before any player revises her strategy.

• % Individuals separated: Time series of the percentage of players who have become single in the current tick.
• Outcome Frequencies: Time series of the fraction of couples where both players cooperated (CC), where one player cooperated and the other one defected (CD), and where both players defected (DD).
• Strategy Distribution: Time series of the distribution of strategies in the whole population. The strategies shown in this plot (and their color) can be chosen by the user using the input box plot-the-following-strategy-names-and-colors. The user should input a list of two-item lists, one for each strategy to be plotted. The first item in each two-item list is the name of the strategy to be plotted and the second item is the color for the strategy. For instance:
  

  [ ["C-C-D-C-D" 87] ["C-C-L-C-D" 94] ["D-C-L-L-C" green] ["D-D-D-D-D" red] ]

  Colors can be determined using either names or numbers, according to NetLogo's 'Color Swatches', which can be accessed through the Tools menu.
• Action with new partner: Time series showing the fraction of players who play C or D when they first meet a partner (i.e. the first gene).
• Avg Payoff: Time series showing the average payoff of all the players and also of those who started a new partnership in the current tick (new couples).
• Action after CC: Time series showing the fraction of players who, after outcome CC, choose to stay and cooperate (Stay-C), stay and defect (Stay-D), leave and start the next partnership cooperating (Leave-C) or leave and start the next partnership defecting (Leave-D).
• Action after CD: Time series showing the fraction of players who, after outcome CD, choose Stay-C, Stay-D, leave and start the next partnership cooperating (Leave-C) or leave and start the next partnership defecting (Leave-D).
• Action after DC: Time series showing the fraction of players who, after outcome DC, choose Stay-C, Stay-D, Leave-C or Leave-D.
• Action after DD: Time series showing the fraction of players who, after outcome DD, choose Stay-C, Stay-D, Leave-C or Leave-D.

LICENCE

ES-1-outcome (Endogenous Separation conditioned on the previous outcome) is a model designed to formally analyze the mechanism of endogenous separation (or conditional dissociation) in the evolutionary emergence of cooperation.
Copyright (C) 2025 Luis R. Izquierdo, Segismundo S. Izquierdo & Robert Boyd

This program is free software; you can redistribute it and/or modify it under the terms of the GNU General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version.

This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU General Public License for more details.

You can download a copy of the GNU General Public License by clicking here; you can also get a printed copy writing to the Free Software Foundation, Inc., 51 Franklin Street, Fifth Floor, Boston, MA 02110-1301, USA.

Contact information:
Luis R. Izquierdo
University of Burgos, Spain.
e-mail: lrizquierdo@ubu.es

MODELLERS

This program has been designed and implemented by Luis R. Izquierdo, Segismundo S. Izquierdo & Robert Boyd.